Probleme der Funktionstheorie

Worin liegen denn nun eigentlich die Probleme der Methode? Es lassen sich neben etlichen Details einige Grundprobleme dingfest machen, die die Funktionstheorie mit sich bringt und zuweilen zu Ergebnissen führen, die offensichtlich völlig an der Sache vorbeigehen. Besonders problematisch wird es, wenn Hörerfahrung und Analyseergebnis nicht in Einklang stehen und man nicht dieses an jener, sondern umgekehrt misst. Nicht selten folgt dann der Versuch, das Hören zu manipulieren, indem behauptet wird, man „müsse es eben so hören“. Ein der Wahrnehmung nach sehr einfaches und vertrautes Phänomen wird so umständlich chiffriert, dass der gutgläubige und lernwillige Leser geneigt ist, von der Diskrepanz statt auf die Schwäche der Methode auf sein noch unzureichend sensibilisiertes Wahrnehmungsvermögen zu schließen.

Die Funktionstheorie geht von der Annahme aus, dass Musik, sofern sie denn tonal ist, aus nichts anderem als Kadenzen besteht. Diese Ansicht geht natürlich auf Jean-Philippe Rameau zurück und reflektiert tatsächlich eine der prägendsten Eigenschaften der Tonsprache seiner Zeit: Denn mit der Kodifizierung der Oktavregel um 1700, an der Rameau sich abarbeitet und die ja, wie Ludwig Holtmeier gezeigt hat¹, letztlich eine Verschachtelung von Kadenzmodellen darstellt, kommen jenseits von Sequenzmodellen sämtliche nicht-kadenziellen Fortschreitung endgültig außer Mode.
Rameaus Fundamentalbass unterlegt im Grunde jeder Klangfolge eine potenzielle Bassklausel. Die zweite Kadenzform, dessen Bassklausel statt einer Quinte um eine Quarte fällt – die plagale Cadentia minor – muss er natürlich ebenfalls in sein System integrieren: sie wird zur cadence irréguliere mit Sixte ajoutée. Sämtliche Sequenzmodelle gelten als Aufeinanderfolge geflohener Kadenzen, welches spätestens beim Fauxbourdon zu einem einigermaßen absurden Fundamentalbass führt. Und nicht zufällig sind es eben die Sequenzen, die verbliebenen nicht-kadenziellen Satzmodelle, die auch der Funktionstheorie Probleme bereiten. Denn diese hält eigentlich nur Begriffe für kadenzvorbereitende (Subdominante bzw. Subdominantparallele), Penultima- (Dominante) und Ultima-Klänge (Tonika) bereit. Verlegenheitsbegriffe wie „Tonikagegenklang“ erscheinen allerhöchstens bei trugschlüssigen Wendungen plausibel, wo der jeweilige Klang tatsächlich die Tonika „vertritt“. Wohl kaum jemand wird bestreiten, dass die Symbole der Funktionstheorie die Gesetzmäßigkeit und Funktion etwa der folgenden Klangprogressionen völlig entstellt.




Ein weiteres Grundproblem der Funktionstheorie ist, dass der erdachte Grundton eines Akkords nicht alteriert werden kann, ohne dass dies weitreichende Konsequenzen für dessen Deutung hat. Durch den Generalbass, der die Intervallstruktur beschreibt, geht hingegen der Hintergrund des Gerüstsatzes vor dessen Chromatisierung, also wört. „Einfärbung“, nie verloren. Folgende Beispiele mögen dies demonstrieren.


Dargestellt ist eine einfache Allerweltsformel, der sogenannte phrygische Halbschluss. Phrygisch, da es sich um eine mi-Kadenz handelt, bei welcher die Tenorklausel einen Halbtonschritt absteigt (fa-mi) und die Sopranklausel einen Ganztonschritt hinauf. Im zweiten Fall die Sexte, die auf der Penultima entsteht, erhöht (übermäßig). Es entsteht der berühmte übermäßige Sextakkord, unverzichtbar in beinahe jeder barocken italienischen Oper und jedem klassischen Sonatensatz. Dieser kleine chromatische, satztechnisch folgenlose Eingriff führt dazu, dass die vormals angenommene Subdominante mit Terz im Bass sich in ein absolut wirres Gebilde verwandelt – die einfache Hörwahrnehmung eines Unbedarften soll einer „verkürzten Doppeldominante (ohne Grundton) mit Septime und tiefalterierter Quinte“ entsprechen. Spätestens an diesem Punkt ist aus Aufklärung Vernebelung geworden.


Die Generalbass- und Bassstufenanalyse zeigt die Verwandtschaft der beiden Notenbeispiele. In beiden Fällen schreitet der Bass von der ersten zur fünften Stufe abwärts. Von einem perfekten Klang ausgehend gelangt man über einen imperfekten Sext- in einen dissonanten Septakkord, dessen Septime sich in die Sexte und diese daraufhin in die Oktave auflöst. Die chromatische Alteration der Sexte im zweiten Beispiel wird durch das entsprechende Vorzeichen in der Bezifferung gekennzeichnet.
In folgendem Beispiel haben wir eine ähnliche Situation:


Hier ist die vierte Tonleiterstufe beim zweiten Mal chromatisch erhöht, was in der Bassstufen-Analyse durch eine 4# („erhöhte vierte Stufe“) gekennzeichnet wird. Der Akkord darüber ändert sich dadurch nicht prinzipell: als Quintsextakkord ist er in beiden Fällen ein spannungsreicher Klang, welcher eine Fortschreitung des Basses aufwärts in die fünfte Stufe provoziert. Diese Fortschreitungstendenz erscheint durch die Chromatisierung lediglich graduell geschärft.
In der Funktionsanalyse verwandelt sich die „Subdominante mit Sixte ajoutée“ in eine „Doppeldominante mit Septime und Terz im Bass“, was den Anschein erwecket, es handele sich um zwei völlig unterschiedliche Gebilde. Deren enge Verwandschaft, die dem Hören nach jedem vertraut ist, kann die Funktionstheorie nicht zum Ausdruck bringen.


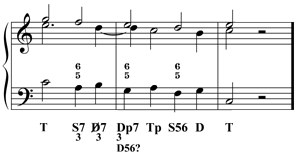
Dieses letzte Beispiel ist ein Ausschnitt des vor allem als „Pachelbel“ oder „Romanesca“ bekannten Sequenzmodells (3-5-Satz):


Liest man die Funktionssymbole, ist man im ersten Fall geneigt, einen Trugschluss von Takt 1 auf 2 anzunehmen – schließlich ist die Verbindung D - Tp (bzw. tG) die einzige Form von Trugschluss, die in der Harmonielehre bis zum Erbrechen gelehrt wird. Da es sich inmitten eines Sequenzmodells gar nicht um irgendeine Art von Schluss handeln kann, wäre diese Auffassung natürlich vollkommen sinnfrei.


Im zweiten Beispiel ist der Basston chromatisch alteriert. Das Modell bleibt erhalten, doch plötzlich hat sich in unserem harmlosen 3-5-Satz eine „verkürzte Zwischendominante mit Septime und Terz im Bass“ eingenistet. Wieder suggeriert uns die Funktionsanalyse eine angesichts dieses elementaren, allein aus 3-5-Akkorden bestehenden Satzmodells eine viel zu komplizierte Situation. Die umständliche Bezeichnung verleitet dazu, dem Phänomen eine weitaus höhere Bedeutung bzw. Komplexität beizumessen, als es eigentlich verdient – man verwechselt die Kompliziertheit der Methode mit der Komplexität der Sache.

¹ Ludwig Holtmeier, »Zum Tonalitätsbegriff der Oktavregel«, in: Systeme der Musiktheorie, hg. von Clemens Kühn und John Leigh, Dresden, 2008